Hello, this is the second post in the #Language series. The first post was about understanding probabilities such as joints, marginals and conditional probabilities using english letters. We were able to answer questions such as:
- What is the most common occuring english letter in all english words ?
- What is the most likely next letter given that the current letter i’m observing is say ’e’ ?
- What was the most likely previous letter given that the current letter i’m observing is say ‘j’ ?
- What is the probability of occurence of a letter pair such as say ’th’ in any english word ?
- What is the probability that an english word starts with the letter say ‘k’ ?
- What is the probability that an english word ends with a letter say ‘w’ ?
In this post, we analyze the characteristics of english words in terms of their word length distribution, and at the end, we combine the results of the previous post (Language I),to build an english text generator using a markov chain model.
Word Length distribution Link to heading
The word length is defined as the number of characters making up an english word. Since english words will have different word lengths, we are interested in “summarizing” this information using a statistical distribution.The graph for the distribution of word lengths for various english words is shown below:
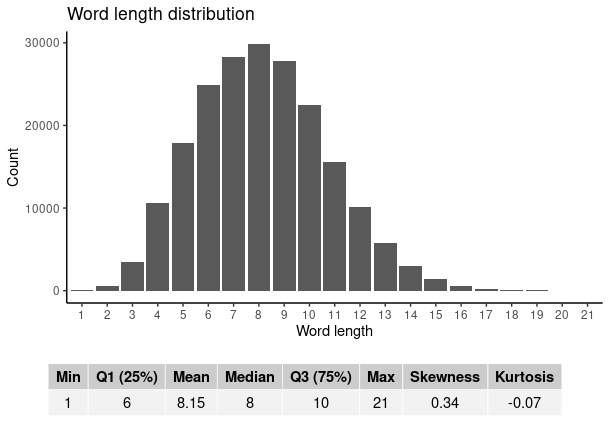
The word length distribution is positively skewed (skewness: 0.34) having a mean of 8, implying most english words have on average a length of 8 characters. The shortest english word was a one character word, such as: i, a, and the longest english was 22 characters long, being: chromophotolithograph1.
The quantiles (1st, 2nd, 3rd) inform that:
- 25% of english words have a maximum possible length of 6 characters.
- 50% of english words have a maximum possible length of 8 characters.
- 75% of english words have a maximum possible length of 10 characters.
For modeling the word length, we only restrict ourselves to discrete statistical distributions since word length is a discrete variable.
If $X$ is the discrete variable representing the word length, then a possible model for word length is the poisson distribution.
The Poisson distribution: Link to heading
The Poisson distribution is a discrete distribution commonly used to model counts of events that occur at a certain rate, such as the number of customers who enter a store in an hour or the number of phone calls received by a call center in a day. In the case of word lengths in a novel, you can think of each word as an event that occurs independently, with a certain probability of occurring at each position in the text.
The probability mass function (PMF) of the Poisson distribution is given by:
$$P(X = k) = \frac{e^{-\lambda}\lambda^k}{k!}, \hspace{2 mm} k = 0, 1, 3, …$$
where $X$ is the random variable representing the number of events, $\lambda$ is the average rate at which the events occur, and k is the number of events that occur in the interval.
For word length modeling however, we will have to use a modification to the poisson distribution to account for the fact that, word length cannot be 0, hence we need a modified poisson distribution for positive integers (starting at 1). Such a distribution exists and is called the Zero-truncated Poisson distribution (ZTP).
“It is the conditional probability distribution of a Poisson-distributed random variable, given that the value of the random variable is not zero. Thus it is impossible for a ZTP random variable to be zero.”
- Source: Wikipedia
The mean and variance of the ZTP distribution are:
$$\mu = \frac{\lambda e^{\lambda }}{e^{\lambda} - 1}$$ $$\sigma^2 = \mu(1 + \lambda - \mu) $$
where $\mu$ is the mean and $\sigma^2$ is the variance.
A markov process is simply a process, where-by the most optimal prediction for the future state, depends only on the process’s current state. Put simply, if a process is markov, then the best prediction for the process at time $i+1$ only depends on the value of the process at time $i$, without reference to past history. Formally: $$P(X_{t+1} = x_{t+1} | X_t = x_t, …, X_1 = x_1, X_0 = x_0) = P(X_{t+1} = x_{t+1} | X_t = x_t)$$ We use this model for text generation as follows:
- We first start by generating a random number $(n)$ from the fitted Word length distribution. This generated number will be the word length input into the markov text generator.
- We initialize the word (find the starting letter), by sampling from the ‘word-starters’ probability distribution. In sampling, we use the ‘word-starters’ probabilities as the sampling weights.
- Since we have the first letter, we now initiate the markov process text generator, which performs the following:
- Step 1: Using the previously generated letter only, we sample randomly letters ‘a’ to ‘z’, where the sampling weights are the Conditional probabilities: $P(Next | Current = *)$.
- Step 2: We repeat step 1 above, until the number of characters generated equals the word length $(n)$
- We return the generated word
Generated results are shown below:
[1] "dorypef"
[1] "batedoralyrophe"
[1] "tamineriextaro"
[1] "ileditritll"
[1] "uberonasidfig"
[1] "brissu"
[1] "tuncierbotind"
[1] "pridemen"
[1] "lobrnesncys"
[1] "ipedngonteese"
[1] "felollynppisala"
[1] "charsukecot"
[1] "scopigickmil"
[1] "titenanh"
[1] "squneracoe"
[1] "vacanchuf"
[1] "eytrincusetin"
[1] "khatilerad"
[1] "rageerphyllylo"
[1] "rymindou"
[1] "mantrsul"
[1] "praleslirido"
[1] "calki"
[1] "rrodessstoum"
[1] "rbislen"
[1] "glluapr"
[1] "delationespete"
[1] "indeecalirrext"
[1] "ppakineepomoi"
[1] "screinec"
[1] "ronesiondan"
[1] "dirmentuthysic"
[1] "taronnnate"
[1] "glliered"
[1] "praberendie"
[1] "ancatelat"
[1] "caspelyelll"
[1] "zontchoma"
Not bad, eh ?
-
what about the 27 character ‘antidisturblishmentarialism’ ? ↩︎